One of the most exciting areas of technology development, but that doesn’t get a ton of mainstream media coverage, is the race to build a working quantum computer that exhibits “below threshold quantum computing” — the ability to do calculations utilizing quantum mechanics accurately.
One of the key limitations to achieving this has been the sensitivity of quantum computing systems — in particular the qubits that capture the superposition of multiple states that allow quantum computers to exploit quantum mechanics for computation — to the world around them. Imagine if your computer’s accuracy would change every time someone walked in the room — even if it was capable of amazing things, it would not be especially practical. As a result, much research to date has been around novel ways of creating physical systems that can protect these quantum states.
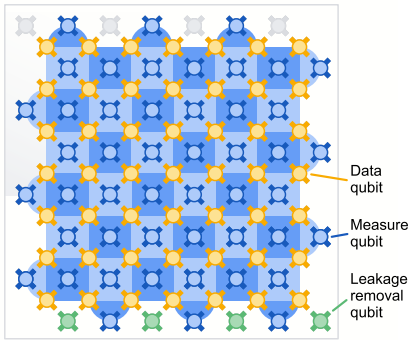
Google has (in a pre-print in Nature) demonstrated their new Willow quantum computing chip which demonstrates a quantum error correction method that spreads the quantum state information of a single “logical” qubit across multiple entangled “physical” qubits to create a more robust system. Beyond proving that their quantum error correction method worked, what is most remarkable to me, is that they’re able to extrapolate a scaling law for their error correction — a way of guessing how much better their system is at avoiding loss of quantum state as they increase the number of physical qubits per logical qubit — which could suggest a “scale up” path towards building functional, practical quantum computers.
I will confess that quantum mechanics was never my strong suit (beyond needing it for a class on statistical mechanics eons ago in college), and my understanding of the core physics underlying what they’ve done in the paper is limited, but this is an incredibly exciting feat on our way towards practical quantum computing systems!
The company’s new chip, called Willow, is a larger, improved version of that technology, with 105 physical qubits. It was developed in a fabrication laboratory that Google built at its quantum-computing campus in Santa Barbara, California, in 2021.
As a first demonstration of Willow’s power, the researchers showed that it could perform, in roughly 5 minutes, a task that would take the world’s largest supercomputer an estimated 1025 years, says Hartmut Neven, who heads Google’s quantum-computing division. This is the latest salvo in the race to show that quantum computers have an advantage over classical ones.
And, by creating logical qubits inside Willow, the Google team has shown that each successive increase in the size of a logical qubit cuts the error rate in half.
“This is a very impressive demonstration of solidly being below threshold,” says Barbara Terhal, a specialist in quantum error correction at the Delft University of Technology in the Netherlands. Mikhail Lukin, a physicist at Harvard University in Cambridge, Massachusetts, adds, “It clearly shows that the idea works.”
‘A truly remarkable breakthrough’: Google’s new quantum chip achieves accuracy milestone
Davide Castelvecchi | Nature News

Leave a Reply